Moving Boundaries in Food Engineering

In studying transport phenomena in foods, the heat, mass, and momentum transfer occurring at the boundaries of a food offer intriguing problems for food engineers.

It is common to encounter these types of problems either at the stationary boundary at the surface of a food, or at moving boundaries within the food, i.e., the freezing front in a food during the freezing process. A fundamental understanding of the transport phenomena at the boundaries is often a prerequisite to developing computer-aided simulation models for improving processes and determining design specifications and operating conditions of processing equipment. This article will examine a variety of food processing systems where these types of problems at the boundaries have major implications on heat and mass transfer processes.

A boundary is defined by the Collins Dictionary as a “a dividing line that indicates the farthest limit.” In processing of foods, we often bring a food into contact with a heating/cooling medium whose properties differ by several orders of magnitude from those of the food. At the interfacial boundary where the food and the process medium meet, the transport processes of heat, mass, and momentum are largely influenced by surface conditions. 

Consider the food sterilization process used in canning. The walls of a metal container provide a boundary around the food contained within the can. The physical properties of the metal wall of the can differ from the properties of the medium used in heating the can. If steam is used as a heating medium, the condensing vapors on the metal surface result in a significantly higher heat transfer than if hot water is used to heat the cans. Inside the can, if we have solids suspended in a liquid, e.g., meatballs in a sauce, and the can is turning on its axis as it moves through a retort, then the heat transfer at the boundary between the sauce and the meatball requires careful examination. The heat transfer coefficient at the surface boundary of the meatball would largely control the amount of heat entering the meatball. This coefficient must be known to calculate a desirable thermal process. In aseptic processing systems, a quantitative knowledge of the surface heat transfer coefficient around a solid particulate as it travels within a liquid in a heat exchanger becomes essential in designing thermal processes. Food engineers have made major progress in these areas during the last decade, but much remains to be done (Baptista, 1997). 

The preceding example illustrates problems associated with a stationary boundary. Now let us consider an example where the boundary moves during a process. This phenomenon is easily observed during freezing of food materials. When a food is surrounded by a medium at subfreezing temperatures, it begins to freeze (Fig. 1). After some time elapses, there are two regions present within the food, a frozen region and an unfrozen region. Over more time, the boundary between the frozen and unfrozen regions moves toward the center of the food. Both these regions have significantly different thermophysical properties. The heat transfer mechanisms across the moving boundary must account for the latent heat of fusion generated at the moving boundary as water is converted into ice. The velocity and shape of this moving boundary is important in designing the process, the freezing equipment, and the quality attributes of the final frozen food. 

The surface heat transfer coefficient h at the static boundary on the surface of the food controls the amount of heat and mass transfer from the food to the cooling medium. If the food is being frozen in a cryogenic freezer, the spray of the cryogen results in higher heat transfer than if the food is in an air blast freezer or in a chamber with slow-moving low-temperature air. Therefore, in freezing, the heat and mass transfer processes occurring at the static surface boundary and the internal moving boundary are critical to our understanding of the process. 

--- PAGE BREAK ---

Predictive Modeling
A predictive modeling approach can be used to systematically study some of the important issues in designing food processes. It comprises six steps:
1. State the problem and its rationale.

2. Develop a mechanistic understanding of the process.

3. Develop a mathematical basis for the process.

4. Implement the mathematical formulation on a computer.

5. Incorporate data on food properties into the model.

6. Validate the predictive model with selected experiments. 

In the following discussion, it will become obvious that in contrast to empirically based methods, the predictive modeling approach does not require experimental data on heat and mass transfer. Instead, the model development is based on the physics of the process, and the “food” is introduced into the model through the values of its properties. Only in step 6 are selected trials conducted to determine heat and mass transfer to validate the model. Because this approach is not product dependent in its initial development, it has more universal applications; additional foods may be examined once we know their properties. Above all, the predictive approach provides a fundamental understanding of the mechanisms involved.

• Immersion Frying of Potatoes. First, we will consider the process of immersion oil frying of foods. The rationale for studying this process is that heat transfer and mass transfer occurring during frying have a major influence on the final product quality (Ashkenazi et al., 1984). The development of the crispy and crunchy texture of fried foods is often one of the most desirable sensory attributes. For example, French fries are popular for their crunchy surface and soft interior. At the same time, there are nutritional concerns related to oil migration into the food during frying. 

Frying is one of the few food processes where the heating medium becomes a major part of the final processed product, up to 35% in the case of potato chips and 15% in French fries. The properties of the oil change during the frying process, thus influencing how it heats the immersed food. During the post-frying period, moisture migration from the soft and moist interior to the surface can alter the crunchy outer region into a soggy texture that is considered undesirable. Knowledge of the kinetics of these processes is necessary to improve the process and equipment. 

Fig. 2 shows a photograph of a potato strip immersed in a beaker containing oil at 180 C at different times of frying. Within the first 2–3 sec, heat begins to enter the surface of the potato strip. Soon after, the internal water, which is converted into water vapor, begins to emerge from the potato strip; a profusion of bubbles leaves the potato strip and rises to the top of the oil reservoir. The thermophysical properties of oil change for several reasons: water vapor condensing within the oil, oxygen from the air mixing into the oil, and the high temperature of the oil itself during the frying process. As a result of these mechanisms, the viscosity of oil increases, and its surface tension changes (Gomes da Silva and Singh, 1995). After a certain amount of use, the oil behaves in a different manner, both as a heat transfer medium and how it migrates into the food. As shown in Fig. 2, the stationary bubbles adhering to the bottom surface of the potato strip tend to decrease the rate of heat transfer, in comparison to heating from the top, where there is considerable turbulence due to the movement of vapor bubbles in the oil (Singh, 1995a). Consequently, the rate of heating for the top and bottom surfaces differs. Furthermore, after about 10 min of frying, no more vapors emerge from the potato strip, indicating that all the water inside the strip has evaporated. 

--- PAGE BREAK ---

Next, we examine scanning electron micrographs of a cross-section of a cylindrical potato strip (1-cm diameter) fried for different lengths of time. As shown in Fig. 3, after 10 sec of frying, there is a thin layer around the circumference that shows a slightly altered structure, most likely due to starch gelatinization in that region. After 20 sec of frying, the outer region shows more of an open and porous structure, with void spaces through which mass transfer begins to take place. This outer region, called the crust layer, becomes more evident after 150 sec of frying, as shown in Fig. 3. 

These observations help us draw an important conclusion: the interfacial boundary between the outer crust and the internal core region moves toward the center as the frying process proceeds. If we continue frying the potato strip for a longer period, such as 20 min, the interfacial boundary will move all the way to the center, and the entire region will become porous. The thermophysical properties of the crust and core regions are considerably different from each other, and they influence the sensory properties of the fried product. The heat and mass transfer processes occurring at the static surface boundary influence the kinetics of the internal moving boundary. Additional experimental observations, using oil colored with oil-soluble dyes and magnetic resonance imaging, have revealed that oil migrates only into the crust region (Farkas et al., 1992). 

The preceding observations help us in developing a schematic diagram of heat transfer (Fig. 4). The rate of heat transfer into the solid food is controlled by the surface heat transfer coefficient at the boundary between the food and oil. The oil migration is only up to the moving boundary interface between the crust and the core region. The moisture present inside the core region evaporates at the moving boundary, and only water vapor transfers through the crust region to the surface of the food. The temperature profile in Fig. 4 indicates that, while the temperature in the oil bath may be constant (shown by AB), there is a temperature drop from B to C, depending on the value of surface heat transfer coefficient. Within the food, the temperature drop from C to D, which is linear in the thin crust region, where the physical properties do not change with temperature. D represents the moving boundary interface, the evaporation front. The water evaporates at temperatures above 100°C, an elevated boiling point because of the presence of solutes in the water (Pravisani and Calvelo, 1986). In the core region, the temperature drop from D to E is nonlinear. As the frying process continues, the crust region expands, as the moving boundary advances toward the center of the food. 

The moving boundary problem, as observed in the frying process, has been an area of interest to mathematicians for more than a century. Stefan (1891) first discussed this problem when studying the freezing and melting of polar ice caps. In the literature, these types of problems are often called the “Problems of Stefan.” These are nonlinear problems, difficult to solve analytically (Crank, 1984). Therefore, numerical solutions have become methods of choice since the availability of computers. 

Using the information gathered regarding the physics of the frying process, we can develop a mathematical description. A set of four partial differential equations are written to describe the heat and mass transfer in the crust and core regions (Farkas et al., 1996a, b). These equations describe the transient change in temperature and moisture within a food as it undergoes frying. The governing equations, along with their initial and boundary conditions, are then solved using numerical procedures. Certain assumptions are made to help simplify the mathematical solution, such as one-dimensional heat and mass transfer (Farkas et al., 1996a). To implement the solution on a computer, numerical methods allow immobilizing the moving boundary at certain instances of time, such as with the use of Landau transformation (Farkas et al., 1996b). <1996A OR B? SEE REFERENCES> 

It should be evident that using the predictive modeling approach up to step 4, no heat and mass transfer data are collected from the food under consideration. It is only in step 5 that the “food” is introduced into the model through its properties. To solve the governing equations, we need properties of the crust and core regions. These properties—thermal conductivity, density, specific heat capacity, diffusivity, and porosity—help identify the uniqueness of the food to the model. In certain cases, these properties may change during the process, and it may be necessary to factor in the property variation with temperature or moisture. Similarly, the heat transfer coefficient at the surface boundary is required. Using the appropriate properties data, we solve the predictive model on the computer. The results sought from the model may be the distribution of temperature, moisture, or growth of the crust layer. 

--- PAGE BREAK ---

Finally, a selected number of validation trials are conducted to measure variables such as temperature or moisture concentration at different locations within the food being fried. The computer-predicted results are then compared with experimental results (Farkas et al., 1996a). Such a comparison is shown in Fig. 5, which shows predicted and experimental temperature profiles. The statistical validation of these comparisons provides confidence in the predictive model. As shown in Fig. 5, the temperature near the surface increases rapidly to near 100 C and, after the moving boundary passes through that location, continues to increase toward the oil temperature. The crust layer experiences temperatures higher than the elevated boiling point of water. This results in several chemical modifications that create the desired aroma and flavor in the fried food. The internal core region remains at temperatures below the elevated boiling point of water, keeping the contents moist and soft. 

The advantages of predictive modeling become obvious when the model is used to predict the performance of a process under different operating conditions. For example, one can model the influence of varying oil temperature, convective heat transfer coefficient, or use of coating with thermophysical properties that have been engineered for desired results (Farkas et al., 1996b). <1996A OR B? SEE REFERENCES> 

In the preceding example on immersion frying, we considered a single moving boundary, that of an evaporation front. However, if we immerse a frozen food directly into heated oil, as is commonly done in processing French fries, then there would be two moving boundaries within the food. The first moving boundary will involve a thawing front moving more rapidly than the second boundary, the evaporation front. Using the predictive modeling approach, we can revise the mathematical development to accommodate the two moving boundaries. In modeling frying of frozen foods, Vijayan and Singh (1997) used an enthalpy formulation to account for the moving boundary representing thawing. This procedure requires knowledge of the enthalpy of a food at different temperatures. As shown in Fig. 6, the center temperature profiles predicted using the model compare well with the experimental measurements. 

• Cooking of Hamburger Patties. The predictive modeling approach described above for frying of frozen potato strips can be adapted to examine an entirely different product and process, i.e., cooking of hamburger patties. The rationale for studying heat transfer in hamburger patties is to develop improved processes that ensure the safety of the cooked product. 

A large amount of ground beef is converted into hamburger patties in the United States. Hamburger patties are cooked in the food industry as prepared meals for retail and institutional markets, in restaurants, and at home. A number of cases related to the survival of Escherichia coli O157:H7 in improperly cooked hamburger patties have led to food poisoning and fatalities. The U.S. Dept. of Agriculture’s Food Safety and Inspection Service requires that the center temperature of hamburger patties must reach 71°C to ensure product safety and FDA has stated that patties should be cooked to 68°C for at least 15 sec. (USDA-FSIS, 1993; FDA, 1993). Because it is impractical to measure the center temperature of every hamburger upon cooking, it is necessary to develop a clear understanding of the transfer process to design equipment and processes that ensure the required safety. Hamburger is a nonhomogenous material; its thermal conductivity, density, and specific heat vary with temperature. Similarly, when the patties are formed, the forming process can create different internal structures of the patty. 

In restaurants, frozen patties are often cooked by directly placing them on heated grills (Fig. 7). The grill temperatures are typically in the range of 170–180°C. Conceptually, we have a situation similar to the example of frying frozen potato strips. There are two moving boundaries within the frozen patty, the thawing and the evaporation boundary, the latter creating the crust region with a firm texture. In addition, there is shrinkage of the patty during the cooking process, with the diameter decreasing dramatically during the cooking process. Previous studies indicate that some of the key factors that influence hamburger cooking are grill surface temperature, fat content of the meat, cooking time, and patty thickness. However, published studies provide limited information needed for optimizing the process or determining the quantitative effect of each of the factors on the patty center temperature. 

--- PAGE BREAK ---

Predictive modeling may be therefore used to develop answers to a variety of questions related to cooking of a hamburger patty: How much variation in the temperature of the contact-heating surface is acceptable without appreciably influencing the patty center temperature? How much variation in patty thickness should be permitted? How much variation in the fat content of the patty may be allowed? When using a two-sided grill (a clamshell grill), how much tolerance in the gap thickness variance may be allowed? What is the influence of the roughness of the grill’s metal surface on heating profiles in a patty? Answers to these questions are important, both to the processors and to the equipment manufacturers. If a one-sided grill is used for heating, the turnover protocol must be such that a required center temperature is achieved (Ikediala et al., 1996). If the patties are cooked on an open gas-fired grill, then the mode of heat transfer at the surface boundary is due to radiation and convection. This would require measurement of convective and radiative heat transfer coefficients. 

Now consider cooking of a hamburger patty in a clamshell grill, where heating is from both sides, although the temperature of the two surfaces may be set at different levels. For a patty that is initially frozen, Fig. 8 illustrates the heat transfer into the patty. At some time of heating, there is the thawing front separating the frozen from unfrozen region, and the evaporating front separating the crust from the internal region. The melting of frozen fat and modification of protein that results in juice release would occur at other temperature fronts as they move through the patty. All these processes take place in a relatively short time—less than 2 min for a 1-cm-thick patty on a clamshell grill. 

The contact boundary between the patty and the grill surface offers interesting problems. The heat transfer coefficient between those two surfaces will depend on the condition of the grill surface (e.g., its roughness) and the surface characteristics of the patty itself. On the bottom surface, as the patty begins to cook and the juices are released from protein, they will begin to fill any voids between the patty and the metal surface. The juices will begin to evaporate, creating steam. Similarly, melted fat will move into the voids, creating thin layers of liquid fat at temperatures close to that of the grill surface. The condition on the top side of the patty may be quite different. The juices and melted fat will move down by gravity, but some may be forced up with steam formed at the bottom surface. Thus, the heat transfer coefficient at the top and bottom surfaces of a clamshell grill may be quite different. This emphasizes the need to obtain reliable data on heat transfer coefficients. 

Assuming the hamburger patty as an infinite slab of L thickness; one-dimensional heat transfer; negligible heat transfer by radiation, chemical reactions, and convection; and thermal properties changing with temperature, the governing equation for the core region can be written as follows (Mannapperuma and Singh, 1988):

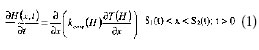
where H is the enthalpy, k_core is the thermal conductivity of the core, T is the temperature, t is the time, and x is the space coordinate perpendicular to the patty plane surface. S₁(t) and S₂(t) are the positions of moving boundaries associated with the evaporation interface and separate the crust region from the core region. Two different moving boundaries are considered to take into account different plate temperatures. This equation is considered valid over the domain where only the thawing process takes place, and the solution of the phase change problem is reduced to the solution of a single problem in terms of enthalpy. 

--- PAGE BREAK ---

The boundary conditions to solve Eq. 1 are:

T = T_b     x = S₁(t), S₂(t); t > 0         (2)

where T_b is the boiling temperature. A uniform temperature is assumed as initial condition:

T = T₀     t = 0; S₁(t) < x < S₂(t)       (3)

Initially, S1(t) = 0 and S2(t) = L. Two further conditions are needed on the moving interfaces to determine their positions (Vijayan and Singh, 1997):

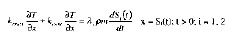
where k_crust is the thermal conductivity of the crust, _v is the latent heat of water vaporization, is the hamburger density, and m is the moisture content. 

The surface temperature can be calculated by equating the heat flux from the plates and the conductive heat flux toward the crust:

        SEE HARD COPY
x =   0; t > 0         (5)

        SEE HARD COPY
x =   L; t > 0         (6)

where h is the contact heat transfer coefficient, while T_p1(t) and T_p2(t) are the plate temperatures that can vary with time. Since the crust thickness is small compared to the slab thickness for the usual cooking times, a linear temperature change in the crust can be assumed. Thus, the heat transfer in the crust region can be approximated by the following relationships (Vijayan and Singh, 1997):

        SEE HARD COPY
x =   0; t > 0         (7)

        SEE HARD COPY
x =   L; t > 0         (8)

The solution of the system (Eqs. 1–8) was obtained numerically using a finite difference method. 

The mathematical formulation for cooking frozen hamburger patties has been developed using Stefan’s approach (Singh et al., 1997) and enthalpy formulation (Voller and Cross, 1981, 1983, 1994). The validation of center temperature predicted with the model and measured experimentally is shown in Fig. 9 (Vijayan and Singh, 1997). Good agreement is observed visually and confirmed statistically. The predictive model was used to answer some of the questions raised previously regarding the design and operation of a clamshell grill. Results show that a variation of 10–20°C in the grill surface temperature does not appreciably influence the center temperature profile. On the other hand, the influence of the gap thickness on the center temperature is significant. As shown in Fig. 10, a 1-mm change in gap thickness may result in a 15°C change in the final center temperature of the patty. 

After having identified the gap thickness as the key parameter, the level of acceptable tolerance in the design of the grill can be determined. Similarly, the model may be used for other scenarios, such as varying the gap thickness during the cooking process and developing criteria for the surface characteristics of the grill to achieve required heat transfer. Studies to address these issues are continuing at the University of California–Davis. 

--- PAGE BREAK ---

Standardized Procedures Needed
It is evident from this discussion that knowledge of food properties is a key requirement in predictive modeling. In this area, although food engineers have made numerous contributions, major deficiencies remain. In the past 20 years, the need for reliable information on food properties has been emphasized in many studies conducted by academia, industry, government, and professional societies. In its report on the needs for the 21st century, the Institute of Food Technologists identified as a top research priority the quality and safety of foods and noted that, to accomplish this task, there is a critical need for information on properties (Rizvi et al., 1993). Unfortunately, we still lack clearly defined standard procedures to measure food properties. 

Several research studies have suggested a variety of methods to measure food properties, and the literature contains a large amount of data on food properties measured using published methods (Rahman, 1995). But the reliability of these data is often questionable because the methods are not standardized, and slight variations in measurement procedures often lead to errors. Therefore, at the beginning of the 21st century, the food engineering community would be wise to agree on standardized methods of measurement for different food properties. The IFT Food Engineering Division may help steer this effort to develop standard procedures and calibration materials for property measurements, similar to the well-accepted AOAC and ASTM methods. Funding for such activity may be solicited from North Central Regional Cooperative Project 136 and USDA–National Research Initiative programs that have identified research on food properties as key funding areas. The need for obtaining reliable food property data extends to the emerging areas of high-pressure, pulsed electric field, ohmic heating, and magnetic pulse processing. Unless standardized procedures are developed, more questionable data will likely be generated. 

Computerized methods, preferably using the Internet, are important in the dissemination of food property data (Singh, 1995b). The efforts of the European Union in this regard are noteworthy. A current project on creating a computerized database of food properties under the auspices of the EU is being conducted, with scientists from 14 countries collaborating. This project is an excellent opportunity for U.S. food engineers to collaborate with their European colleagues to expand the food properties database for global use.

Based on the Food Engineering Division Lecture at the Annual Meeting of the Institute of Food Technologists, Chicago, Ill., July 24–28, 1999.

Research reported in this paper was partially supported by USDA-NRI grants 94-37500-0554 and 98-35503-6453.

by R. PAUL SINGH
The author, a Professional Member of IFT, is Professor of Food Engineering, Dept. of Biological and Agricultural Engineering, University of California, Davis, CA 95616.

Edited by Neil H. Mermelstein
Senior Editor

References