Everything Flows
PROCESSING
Rheology, the science of the deformation and flow of matter, is one of the more fundamental areas of food engineering, with applications in process development, sensory, quality, and product development. The mathematics can be daunting but satisfying as well. Even without a complete understanding of mechanisms, careful and empirical observation can improve process control and operation.
While rheology broadly includes the behavior of both solids and liquids, this article will focus on liquids and other materials that flow, as distinct from those that deform and fracture. Actually, the precise distinction between solids and liquids is not always easy to make.
Measuring Rheological Properties
Among the areas in which rheological data are useful are making process engineering calculations for pipes, pumps, extruders, mixers, and other equipment; determining ingredient functionality in product development; and characterizing products by their rheological properties for quality control purposes.
Fundamental rheological properties are independent of the instrument used to measure them, but some instruments in common use give empirical and subjective values, which nonetheless can be useful. Examples include the Farinograph, Mixograph, and Bostwick Consistometer.
The most familiar rheological property for fluids is viscosity, which is the ratio between the stress needed to shear a fluid held between parallel plates, one of which is stationary and the other moving, and the shear rate, which is the velocity of the moving plate divided by the distance between the plates. For ideal or Newtonian fluids, the viscosity is a constant regardless of shear rate, while for many foods viscosity may be a function of shear rate.
In practical applications, such as pumping or mixing, shear rate is related to the velocity of flow or to the tip speed of a mixer impeller. The stress may be related to the pressure created by a pump or gravity, and to the torque exerted by a mixer impeller. Intuitively, high viscosity is associated with thick, slow-flowing fluids such as honey or starch suspensions, while low viscosity is associated with water and solvents.
Table 1.1 in Rheological Methods in Food Process Engineering by James F. Steffe (see sidebar at end of article) gives values of shear rates (in reciprocal seconds) typical of familiar materials and processes. Some examples are 10–6–10–3 for sedimentation of particles in a suspending liquid; 100–103 for extrusion; 101–102 for chewing food; 101–103 for mixing; and 100–103 for pipe flow. The significance of knowing these ranges is to ensure that fluid property data are taken at the appropriate conditions, since extrapolation of rheological measurements can be inaccurate.
--- PAGE BREAK ---
The determination of fundamental rheological properties involves establishing laminar shear flow in a well-defined geometry and measuring the shear rate and stress. It is important to control temperature, because viscosity changes with temperature, as anyone who has warmed pancake syrup to improve flow has observed. Some common geometries include capillary tubes, cone and plate, parallel disks, and concentric cylinders. Commercially available instruments offer these and some other arrangements.
For non-ideal fluids, other rheological properties can be measured using an instrument called a rheogoniometer. The normal stress is one such property, found in viscoelastic fluids such as polymers.
In measuring the viscosity of foods, it is important not only to control temperature, but also to avoid loss of water, sedimentation of particles, and other reactions that might occur and change fluid properties.
Viscosity is expressed in units of Pascal seconds. One Pa.sec equals 1,000 centiPoise (cP). Examples of some common fluid viscosities at room temperature are gasoline 0.7 cP, water 1 cP, cream 10 cP, vegetable oil 100 cP, and honey 10,000 cP.
Types of Fluids
Some fluids appear to have a yield stress, which means they will not flow until some minimum stress is applied. Yield stress is an idealized concept, because in fact almost all "flowable" materials will eventually flow at low shear rates, but the concept makes some calculations practical. For example, pitch, a petroleum derivative that has been used to waterproof ships and roofs, is so viscous that it shatters if struck by a hammer. Yet it flows at room temperature, but very slowly. A physics experiment/demonstration begun in 1927 (see www.physics.uq.edu.au/pitchdrop/pitchdrop.shtml) consists of pitch in a glass funnel. Only eight drops have fallen in 72 years.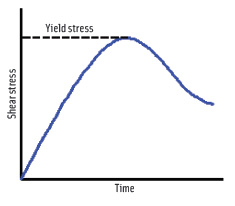 
Many foods have viscosities that are functions of shear rate and often are shear-thinning, meaning that as shear rate increases, the apparent viscosity decreases. One practical consequence is that in laminar pipeline flow, shear-thinning fluids have blunter velocity profiles than do Newtonian fluids. This means that the residence time distribution in a pasteurizer or aseptic process hold tube is different from that calculated for a Newtonian fluid. Fortunately, the result is conservative if the hold tube was sized for a Newtonian fluid, meaning that the hold time for the fastest-moving particle in laminar flow will be longer than it theoretically need be. For heat-sensitive products, this could result in overcooking, so some processes may use the non-Newtonian viscosity relationship, if it is known.
To determine non-ideal fluid properties, stress must be measured over a range of shear rates, preferably the range of potential application. While the data for Newtonian fluids fit a straight line which goes through the origin on a plot of stress against shear rate, non-ideal fluids will generate a curve which may or may not intersect the origin. Various equations have been fit to such data, a few of which are presented in Table 1.3 in Steffe’s book. One of the simplest is the power law, in which the stress is equal to a constant K times the shear rate raised to a power n. If n is <1, the fluid is shear thinning; if n is >1, it is shear thickening. If the data appear to intersect the stress axis at zero shear rate, that value is the yield stress.
--- PAGE BREAK ---
Some fluids have time-dependent viscosities, meaning that with shearing the viscosity appears to decrease or, more rarely, increase. Tomato ketchup can form a gel upon sitting and be hard to pour, but upon being disturbed, the viscosity decreases and the fluid flows. Thus, shaking the bottle before trying to pour can improve flow.
Empirical Measurements
Many empirical measurements of fluid properties have been developed in the food industry. These do not determine fundamental rheological properties but rather measure some index that correlates with product quality or processing conditions. Table 1.5 in Steffe’s book lists many such instruments.
Testing dough for baking of bread, crackers, and cookies is a common application. Dough is one of the more complex fluids encountered in food processing, and its flow properties affect the way it is formed and the texture of the final product.
Typically, the instrument for testing dough is a small mixer with specific geometry. Measured amounts of flour and water are introduced, the temperature is controlled, and the torque required to drive the mixer is measured as a function of time. As dough develops—meaning that the gluten protein in wheat flour becomes hydrated and creates a network enclosing the starch granules—the apparent viscosity increases, causing the torque to increase. The plot is typically jagged and can be difficult to read and interpret. However, the time to peak energy consumption has been found to correlate with dough performance.
Other means of measuring dough include the extension of a cylinder of dough and the blowing of a bubble from a thin sheet.
The Bostwick Consistometer is relatively simple in design and operation but is relied on for testing baby food, tomato products, applesauce, and other foods. It has a compartment separated from a trough by a quick-opening gate. The trough is scored at 0.5–cm intervals. Test material is put into the compartment, the gate is opened, and the flow is observed for a specific time (5–30 sec). The distance traveled is reported as the Bostwick value. This value is difficult to correlate with fundamental properties because the flow occurs under varying shear rates. However, one analysis suggests that the value should correlate with apparent viscosity divided by density raised to the –0.2 power. One concern with the Bostwick instrument as a quality control device is inconsistency in operation. The instrument needs to be on a level surface and observed for a consistent and specific period of time.
Useful Rheology References
Much of this article is based on the text, Rheological Methods in Food Process Engineering, by James F. Steffe, Professor, Dept. of Food Science & Nutrition and Dept. of Biosystems and Agricultural Engineering, Michigan State University, East Lansing (phone 517-353-4544). The book is published by Steffe’s own publishing house, Freeman Press, and is available free at www.egr.msu.edu/~steffe/freebook/offer.html.
Two other useful references on the topic deserve mention. One is Food Engineering, edited by Gustavo V. Barbosa-Cánovas and available in hardcover and electronic form as part of the Encyclopedia of Life Support System (EOLSS) published in 2005 by UNESCO Publishing (www.eolss.net). Section 3 of the book, "Food Rheology and Texture," has nine chapters.
The other book is Handbook of Food Engineering Practice, edited by K.J. Valentas, E. Rotstein, and R.P. Singh and published in 1997 by CRC Press (www.crcpress.com). It has several chapters on rheology.
by J. Peter Clark,
Contributing Editor,
Consultant to the Process Industries,
Oak Park, Ill.
[email protected]